Data Visualization: Matplotlib Exercises

We now have a solid understanding of how to use matplotlib to create fully customizable plots. I've put together a series of exercises to help test your understanding. With each question, I've added a sample Figure displaying a correct solution, as well as one or more hints to help guide you. Good luck!

Please note, that not all the answers to these questions can be found within this tutorial, that's because this tutorial was never meant to exhaustively cover everything matplotlib, rather it was intended to provide foundational skills. To solve these questions, you'll likely need to use the matplotlib official reference.

matplotlib series:

Basic plotting

Customization

The matplotlib API

Exercises (this post)

All the code from this post can be found here

For brevity, assume these statements are included with every solution:

import matplotlib.pyplot as plt
import numpy as np

rng = np.random.deafult_rng(101) # not strictly necessary!

fig, ax = plt.subplots()

COLOR_BLUE = '#1F77B4'
COLOR_ORANGE = '#FF7F0E'
COLOR_GREEN = '#2CA02C'
COLOR_PURPLE = '#9467BD'

Many of these plots use randomly generated data, if you want your plots to look like mine, you can set the seed of the random generator to 101 as I have done.

Exercises 1-4 were selected to test your knowledge of basic plotting and customization with matplotlib.

1: Create a scatter plot using two datasets each consisting of 100 random data points with values between 0 and 1. Use different marker styles and colors for each dataset. Add a title and legend to the plot. Figure 1: Scatterplot of random data

Hint(s)

1. You can use numpy.random.Generator.random((2, 100)) to easily generated 100 random xy datapoints. We've already created the Generator object above with

rng = np.random.default_rng(101)

2. Check Axes.scatter for help making a scatter plot.

Solution

data1 = rng.random((2, 100))
data2 = rng.random((2, 100))

ax.scatter(*data1, marker='*', label='data1') # *data1 = (data1[0], data1[1])
ax.scatter(*data2, marker='o', label='data2')

ax.set_title('Randomly generated data')
ax.legend()

plt.show()

2: Create a pie chart with the following data: sizes = [25, 20, 45, 10] and labels = ['A', 'B', 'C', 'D']. Customize the colors and explode the 'D' slice.

Figure 2: Pie chart with custom colors and exploded slice

Hint(s)

This is simpler than it may seem, Axes.pie already contains an 'explode' parameter. If you need a little more explicit help, refer to this tutorial .

Solution

sizes = [25, 20, 45, 10]
labels = ['A', 'B', 'C', 'D']
explode = [0, 0, 0, 0.2]
colors = [COLOR_BLUE, COLOR_ORANGE, COLOR_GREEN, COLOR_PURPLE]

ax.pie(sizes, explode=explode, labels=labels, colors=colors)

plt.show()

3: Create a subplot with a 2x2 grid, displaying a line plot, scatter plot, bar plot, and histogram using randomly generated data. Customize each plot with a title and appropriate colors, and add a title to the Figure.

Figure 3: Four different plots of random data

Hint(s)

You will need to redefine the fig, ax = plt.subplots() call.
Axes.plot
Axes.scatter
Axes.bar
Axes.hist
numpy.random.Generator.random
You can use numpy.random.Generator.normal(0, 0.1, 100) to generate a normal distribution for the histogram.

Solution

Remember to delete/comment fig, ax = plt.subplots()

fig, axs = plt.subplots(2, 2, tight_layout=True) 
line_data = rng.random((10,))
scatter_data = rng.random((2, 10))
bar_data = rng.random((3,))
bar_labels = ['A', 'B', 'C']
hist_data = rng.normal(0, 0.1, 100)

fig.suptitle('Four different plots of random data', weight='bold')
axs[0][0].set_title('Line plot')
axs[0][0].plot(line_data, color=COLOR_BLUE)
axs[0][1].set_title('Scatter plot')
axs[0][1].scatter(*scatter_data, color=COLOR_ORANGE)
axs[1][0].set_title('Bar plot')
axs[1][0].bar(bar_labels, bar_data, color=COLOR_GREEN)
axs[1][1].set_title('Histogram')
axs[1][1].hist(hist_data, color=COLOR_PURPLE)

plt.show()

Remember to replace fig, axs = plt.subplots(2, 2) with fig, axs = plt.subplots() if you're going to do more exercises in the same file

4: Create a bar plot representing the average sales of a company across four quarters in a year. Add error bars to show the standard deviation. Add a title, labels, custom colors, and a legend.

Figure 4: Made-up Company Sales, with Standard Deviation

Hint(s)

You can use numpy.random.Generator.random to generate the data, you could generate 12 data points, one for each month, 364 data points, one for each day, etc. However you cannot simply generate one data point for each quarter, as then you won't have enough data to calculate standard deviations.
Axes.bar
Axes.errorbar

Solution

sales = rng.random((12,)) # 12 months in a year
quarter_len = len(sales) // 4
quarters = [sales[i:i+quarter_len] for i in range(0, len(sales), quarter_len)]
quarter_avgs = [np.average(x) for x in quarters]
quarter_stds = [np.std(x) for x in quarters]
bar_labels = ['1st', '2nd', '3rd', '4th']

ax.bar(bar_labels, quarter_avgs, color=COLOR_BLUE, label='Average Sales')
ax.errorbar(bar_labels, quarter_avgs, yerr=quarter_stds, fmt='o',
    color=COLOR_ORANGE, label='Standard Deviation')

ax.set_title('Made-up Comapny Sales')
ax.set_xlabel('Quarter')
ax.set_ylabel('Sales ($)')
ax.legend()

plt.show()

Exercises 5-8 were selected to test your ability to create 'non-standard' plots (i.e., plots that require a little more work than just calling Axes.plot_type.

5: Generate random data to simulate the sale of three products over four quarters. Label the products as "Widgets", "Gadgets" and "Gizmos". Create a stacked bar plot of this data, make each product a different color, and add a title, legend, and axis labels.

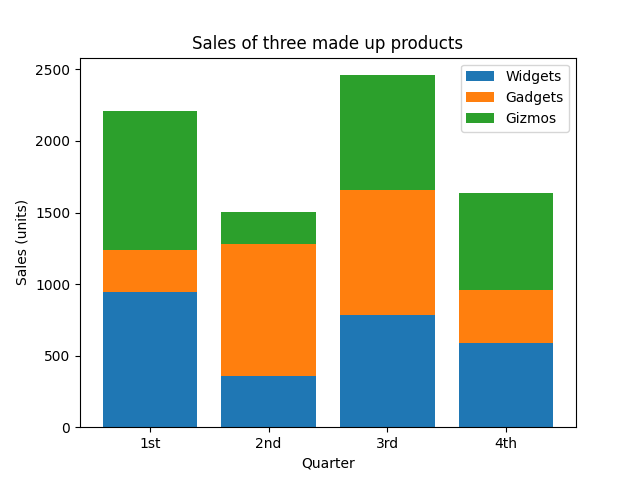
Figure 5: Stacked bar plot

Hint(s)

You won't find an Axes.stackedbar method or anything at the sort, instead take a close look at Axes.bar .

Axes.bar has the bottom parameter, which is set to 0 by default. What if we were to set the bottom according to previous data?

Solution

sales = 1000 * rng.random((3,4))
quarters = ['1st', '2nd', '3rd', '4th']
labels = ['Widgets', 'Gadgets', 'Gizmos']
colors = [COLOR_BLUE, COLOR_ORANGE, COLOR_GREEN]
bottom = np.zeros(len(quarters))
for i, product in enumerate(sales):
    ax.bar(quarters, product, label=labels[i], color=colors[i], bottom=bottom)
    bottom += product

ax.set_title('Sales of three made up products')
ax.set_xlabel('Quarter')
ax.set_ylabel('Sales (units)')
ax.legend()

plt.show()

6: Create a 3D scatter plot using three sets of random data points, each containing 100 points with values between 0 and 1. Customize the plot by using a different marker for each dataset, changing the colors, and adding a title and legend.

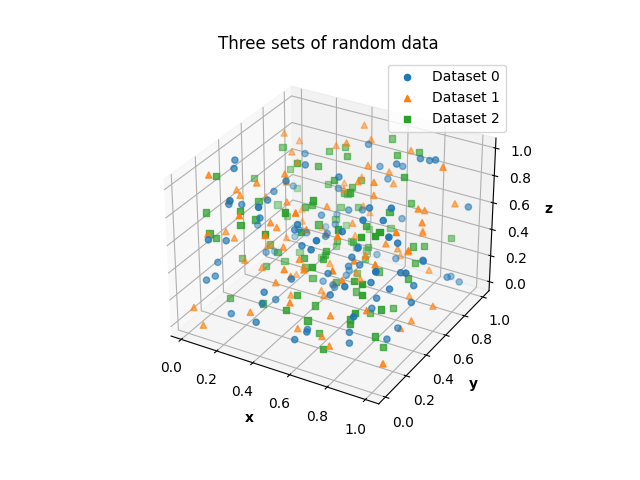
Figure 6: 3D scatterplot

Hint(s)

You'll need to re-define the fig, ax = plt.subplots() call as follows:

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

Once you have a 3D subplot, you can simply call Axes.scatter as before.

Solution

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
data = [rng.random((3, 100)) for _ in range(3)]
markers = ['o', '^', 's']
colors = [COLOR_BLUE, COLOR_ORANGE, COLOR_GREEN]
for i, dataset in enumerate(data):
ax.scatter(*dataset, label=f'Dataset {i}', color=colors[i],
marker=markers[i])

ax.set_title('Three sets of random data')
ax.set_xlabel('x', fontweight='bold')
ax.set_ylabel('y', fontweight='bold')
ax.set_zlabel('z', fontweight='bold')
ax.legend()

plt.show()

7: Generate a 10x10 matrix with random values between 0 and 1. Use this data to generate a heatmap. Change the color maps of the heatmap, and add text to each cell of the heatmap to show its associated value, customize the color of the text and center it both horizontally and vertically. Finally, add a colorbar and a title.

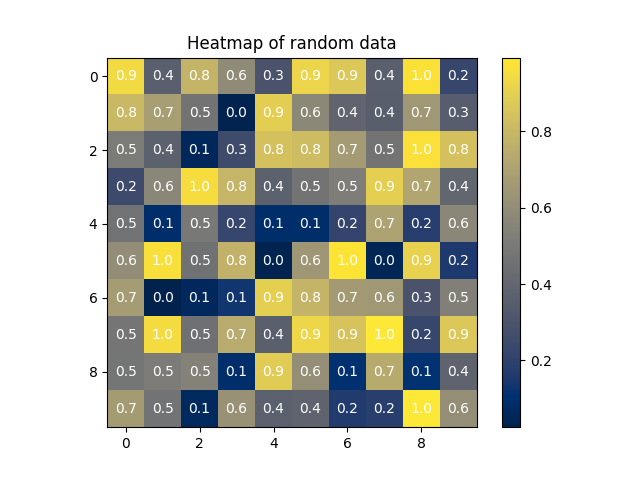
Figure 7: Colormap of random data

(Colormap shown here: cividis)

Hint(s)

You won't find an Axes.heatmap method or anything of the sort. You'll actually need to go digging around in the image processing section of the documentation to solve this one.

The way computers process images are as matricies containing pixel values.

numpy.random.Generator.random
Axes.imshow
matplotlib.colorbar

Solution

data = rng.random((10, 10))
heatmap = ax.imshow(data, cmap='cividis')

for r in range(data.shape[0]):
    for c in range(data.shape[1]):
        ax.text(c, r, np.round(data[r, c], 1), ha='center', va='center', color='white')

cbar = fig.colorbar(heatmap, ax=ax)
ax.set_title('Heatmap of random data')

Exercises 8 and 9 are designed to test your knowledge beyond just matplotlib, specifically your ability to combine your plotting skills with your NumPy skills.

8: Plot an Archimedean spiral

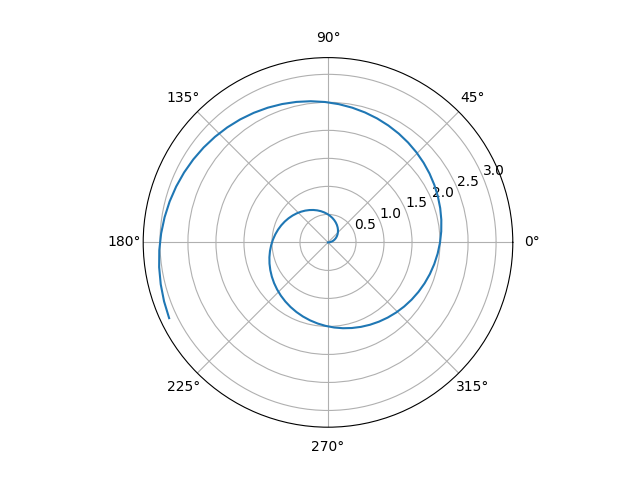
Figure 8: Polar plot of Archimedean spiral

Hint(s)

You will need to re-define the fig, ax = plt.subplots() call in a similar way to exercise 5. Refer to the matplotlib.figure section of the documentation.

Once you've converted the Figure to polar co-ordinates, you can actually use Axes.plot .

In a polar plot, the x-axis represents the angle (θ), and the y-axis represents the distance (r) from the origin.

Solution

fig = plt.figure()
ax = fig.add_subplot(projection='polar')
r = np.linspace(0, np.pi, num=100)
theta = np.pi * r
ax.plot(theta, r)

plt.show()

9: Generate 100 values of a linear function and 'corrupt' it with random Gaussian noise. Plot these data as a scatterplot. Now using only matplotlib and NumPy, perform a Linear Regression on the data and plot the result (i.e. plot a line of best fit). Calculate the R^2 value of the regression. Add a title, legend, and the R^2 value to the plot, and change the color and style of the line representing the regression.

This problem is made easy using seaborn, which is why I've forbidden it from this exercise :). I do plan on eventually writing a seaborn tutorial.

You will find folks online suggesting numpy.polyfit for a problem such as this, however, the official numpy documentation states:

... the poly1d class and associated functions defined in numpy.lib.polynomial, such as numpy.polyfit and numpy.poly, are considered legacy and should not be used in new code.

So try to find a way to solve this problem without using it (free hint: the documentation page I just linked to points to another method you can use!)

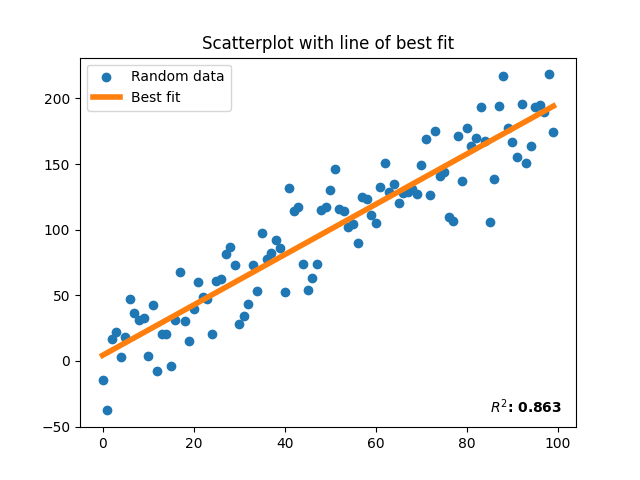
Figure 9: Scatterplot of random data, with a line of best-fit added

Hint(s)

1: To generate the initial data, you can write a linear function and use numpy.random.Generator.normal . Then, just add the random data to the linear function to 'corrupt' it.

2: You can either use numpy.linalg.lstsq or numpy.polynomial.polynomial.Polynomial.fit . Of the two, the Polynomial method is just a tad easier.

3: Both methods above can return the Sum of Squared Residuals (SSR). This is not the R^2 value. However, it is a part of the calculation of R^2:

R^2 = 1 - (SSR / SST)

Where SST is the Total Sum of Squares, you can obtain the SST by:

SST = sum((y - np.mean(y))**2)

Solution

a = np.arange(100)
b = 2 * a + 1 + rng.normal(scale=20, size=100)
ax.scatter(a, b, color=COLOR_BLUE, label='Random data')

# linalg.lstsq solution ==================================================
# linalg.lstsq performs linear regression by finding the closest solution to
# a @ x = b, where x will be a vector containing our least-squares solution.
# because we need x to be a 100x1 vector, we need to convert a to a nx100
# matrix
A = np.vstack([a, np.ones(len(a))]).T
result = np.linalg.lstsq(A, b, rcond=None)
m, c = result[0]
line_of_best_fit = [m*x + c for x in a]

SSR = result[1]
SST = sum((b - np.mean(b))**2)
R2 = 1 - (SSR / SST)

ax.plot(a, a*m+c, color=COLOR_ORANGE, lw=4, label='Best fit')
ax.set_title('Scatterplot with line of best fit')
ax.text(85, -40, f'$R^2$: {R2[0]:.3f}', fontweight='bold')
ax.legend()

plt.show()

# Polynomial.fit solution ================================================
line, full = np.polynomial.polynomial.Polynomial.fit(a, b, deg=1, full=True)
c, m = line.convert()

SSR = full[0]
SST = sum((b - np.mean(a))**2)
R2 = 1 - (SSR / SST)

ax.plot(a, m*a+c, color=COLOR_ORANGE, lw=4, label='Best fit')
ax.set_title('Scatterplot with line of best fit')
ax.text(85, -40, f'$R^2$: {R2[0]:.3f}', fontweight='bold')
ax.legend()

plt.show()

As a reminder this tutorial is not exhaustive, there are many things you can do that we haven't even touched here (have a look at the examples on the official documentation page for some fun ideas!) However if you've completed this tutorial you should have the foundational skills to visualize data in just about any way you can think of.

Posted: 2023-04-18